《预防医学》快递(122)
加强流感监测和预警,及时采取相应防控措施具有重要的公共卫生意义。浙江省疾病预防控制中心传染病预防控制所丰燕等作者利用 2012—2022 年浙江省流感病毒核酸阳性资料建立移动流行区间法(MEM)模型,估算 2022—2023 年浙江省流感流行阈值及强度分级阈值,分析流感流行强度。结果显示,2022—2023 年浙江省流感流行开始阈值和结束阈值分别为 19.32% 和 10.92%,中、高和极高强度阈值分别为 48.65%、63.49% 和 68.47%,2023 年第 8—18 周为流感流行期,其中第 9—14 周处于高、极高流行强度。研究提示 MEM 可用于评估流感流行强度,为早期识别流感流行并采取分级防控措施提供参考。
作者简介
通信作者 | 孙继民 主任医师
浙江省疾病预防控制中心传染病预防控制所所长,《中国媒介生物学及控制杂志》副主编,浙江省预防医学会流行病学专业委员会副主任委员,入选浙江省医坛新秀、浙江省卫生高层次创新人才培养工程等。曾获中华预防医学会科技进步三等奖、浙江省政府科技进步奖二等奖、浙江省医药卫生科技进步特等奖等多项荣誉。长期从事急性传染病特别是虫媒及动物源性传染病研究。

第一作者 | 丰燕 主管医师
浙江省疾病预防控制中心传染病预防控制所,主要从事传染病防制相关工作。
【引用本文】丰燕,徐增豪,凌锋,金家列,王笑笑,尚晓鹏,孙继民.应用移动流行区间法分析2012—2023年浙江省流行性感冒流行强度[J].预防医学,2024,36(10):829-833.DOI:10.19485/j.cnki.issn2096-5087.2024.10.001
摘要
目的 应用移动流行区间法(MEM)估算 2012—2023 年浙江省流行性感冒(流感)的流行阈值和分级强度阈值,评估流感流行强度,为浙江省流感防控提供参考。方法 通过中国流感监测信息系统收集 2012—2022 年浙江省流感流行季(第 40 周至次年第 20 周)流感病毒核酸阳性率资料,建立 MEM 模型,采用交叉验证法筛选最优模型;利用最大累积和百分比函数划分流行前期、流行期和流行后期,估算流感流行阈值及强度分级阈值,并评估 2022—2023 年流行季浙江省流感流行强度。结果 2012—2022 年有 5 个流感流行季的流感病毒核酸阳性率数据纳入模型,参数 δ 取 1.5 时 MEM 模型表现最优,灵敏度为 0.971,特异度为 0.745,约登指数为 0.716。模型分析结果显示,2022—2023 年流行季浙江省流感流行开始阈值和结束阈值分别为 19.32% 和 10.92%,中、高和极高强度阈值分别为 48.65%、63.49% 和 68.47%。由此评估 2022 年第 40 周—2023 年第 7 周为流感流行前期;第 8—18 周为流感流行期,其中第 8 周处于低流行强度,第 9 周达到高流行强度,第 10—13 周处于极高流行强度,第 14 周、第 15 周分别回落至高流行和中流行强度,第 16—18 周降至低流行强度;第 19 周后处于流行后期。结论 MEM 可用于评估流感流行强度,为早期识别流感流行并采取分级防控措施提供参考。
【关键词】流行性感冒;移动流行区间法;流行强度;流行阈值
前言
流行性感冒(流感)传染性强,传播迅速,病毒易变异,人群普遍易感,引起暴发和流行。流感的季节性流行造成全球严重的疾病负担,据统计,每年约有 10 亿例季节性流感病例,其中包括 300 万~500 万重症病例,导致 29 万~65 万人死亡[1]。因此,加强流感监测,及时预测流感流行和分级评估流行强度,并采取相应级别的防控措施具有重要的公共卫生意义。由于流感流行具有地区差异,在温带地区表现为每年冬春季的季节性流行和高发,在热带地区呈多样化[2-4],因此需制定不同的流感流行阈值和分级评估标准。移动流行区间法(moving epidemic method,MEM)由西班牙学者 VEGA 等[5]提出,已被应用于多种传染病的流行强度评估[6]。浙江省自 2009 年建立覆盖全省的流感监测网络,至 2023 年共建立包含 16 家国家级哨点医院和 13 家网络实验室,根据国家流感监测方案全年开展流感监测。本研究利用 2012—2023 年浙江省流感监测数据,建立 MEM 模型计算流感流行阈值及不同流行强度分级阈值,评估流感流行强度,为浙江省流感防控工作提供参考。
。
1 资料与方法
1.1 资料来源 资料来源于中国疾病预防控制信息系统中国流感监测信息系统,以周为单位,收集 2012—2023 年浙江省国家级流感哨点医院流感监测数据。
1.2 方法
1.2.1 MEM 模型建立 流感监测有 2 个重要指标:流感样病例(influenza-like illness,ILI)百分比(ILI%),即 ILI 病例数占同期门急诊就诊病例数的比例;流感病毒核酸阳性率,即 ILI 中流感病毒核酸检测阳性数占 ILI 检测数的比例。ILI% 易受其他呼吸道病毒影响,而流感病毒核酸阳性率更能准确反映流感流行强度[7],因此作为本研究流感流行强度的评估指标。采用 WPS 2023 软件建立浙江省周流感病毒核酸阳性率数据库,采用 R 4.3.1 软件 mem 程序包建立 MEM 模型。
MEM 模型建议纳入 3~10 个流行季的数据,流行季数量过多会降低模型拟合优度,过少则无法真实反映研究地区的流感流行水平;同时要求流感呈单峰流行[5]。参考既往研究[8-9],剔除受新型冠状病毒感染疫情防控措施影响较大的 2019—2021 年 2 个流行季,本研究选择浙江省 2012—2022 年 8 个冬春流行季(第 40 周至次年第 20 周)的流感病毒核酸阳性率数据建立 MEM 模型。
MEM 建模分为 3 步:第 1 步,确定流感流行季中的流行前期(流感流行季开始至流感流行期前)、流行期(流感流行开始至结束)和流行后期(流感流行期结束至流感流行季结束)。根据流感流行规律,从专业角度确定流感流行季的起止时间和时长,采用最大累积和百分比(maximum accumulated rates percentage,MAP)函数划分流行前期、流行期和流行后期[5-6]。最大监测指标累积和占流行季监测指标累积和的百分比首次低于预先设定的阈值(即参数 δ)的时间段定义为流行期,流行期的长度为具有 MAP 的连续最少周数。本研究中,MAP 指在一个流感流行季内,一段时期内流感病毒核酸阳性率的累积和占流行季总流感病毒核酸阳性率累积和的百分比的最大值,公式如下:
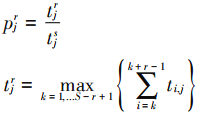
式中,r 为周数;k 为连续 r 周的起始周次数;k+r-1 表示连续 r 周的结束周;j 表示第几个流行季,取 1~N 之间的流行季整数,N 为纳入分析的流感流行季数;S 为每个流行季的监测周数;prj 为第 j 个流感流行季的连续 r 周内的流感病毒核酸阳性率累积和占总累积和的相对最大值;trj 为第 j 个流感流行季的连续 r 周的流感病毒核酸阳性率累积和的相对最大值;tsj 为第 j 个流感流行季的流感病毒核酸阳性率累积和;ti,j 为第 j 个流感流行季第 i 周的流感病毒核酸阳性率。
第 2 步,计算流行阈值。根据流行前期和流行后期的流感病毒核酸阳性率数据分别计算流行开始阈值和流行结束阈值。选择每个流感流行前期流感病毒核酸阳性率最大的前 n 个值纳入分析(n=30/N),计算这 30 个值的算数均数的 95%CI 上限作为流行开始阈值;采用相同方法,利用流行后期流感病毒核酸阳性率数据计算流行结束阈值。
第 3 步,计算流行强度分级阈值。利用流行期流感病毒核酸阳性率数据计算流行强度分级阈值。选择每个流感流行期流感病毒核酸阳性率最大的前 n 个值纳入分析(n=30/N),计算这 30 个值的几何均数的 50%CI、90%CI 和 95%CI 上限,依次作为中、高和极高强度阈值。
通过以上步骤得到的阈值与监测的实际值进行比较,以评估流行强度,分为 5 个等级:(1)非流行期(流行前期和流行后期),周流感病毒核酸阳性率<流行开始/结束阈值;(2)低流行强度,流行开始阈值≤周流感病毒核酸阳性率<中强度阈值;(3)中流行强度,中强度阈值≤周流感病毒核酸阳性率<高强度阈值;(4)高流行强度,高强度阈值≤周流感病毒核酸阳性率<极高强度阈值;(5)极高流行强度,周流感病毒核酸阳性率≥极高强度阈值。
调整参数 δ。VEGA 等[5]建议参数 δ 范围为 2.0~4.0,国内多数研究选择 3.0 以下[7-8,10-11]。本研究采用穷举法,参数 δ 起始值设为 1.0,结束值设为 3.0,步长设为 0.1,依次建模,选择灵敏度、特异度和约登指数综合表现最优时对应的 δ。
1.2.2 MEM 模型评价及应用 采用交叉验证法评价模型效果。每个流行季单独作为目标流行季,其他流行季作为历史基线数据,应用 MEM 模型第 1 步和第 2 步计算目标流行季的流行开始/结束阈值,将流行季各周的实际流感病毒核酸阳性率与 MEM 模型划分的流行前期、流行期、流行后期及流行开始/结束阈值进行比较,计算灵敏度、特异度和约登指数。真阳性周:该周为流行期,流感病毒核酸阳性率>流行开始/结束阈值;真阴性周:该周为流行前/后期,流感病毒核酸阳性率<流行开始/结束阈值。灵敏度=真阳性周数/流行期总周数;特异度=真阴性周数/非流行期总周数;约登指数=灵敏度+特异度-1。选择灵敏度、特异度和约登指数综合表现最优的模型,计算流行阈值和分级强度阈值,评价 2022—2023 年浙江省流感冬春流行季的流行强度。
2 结果
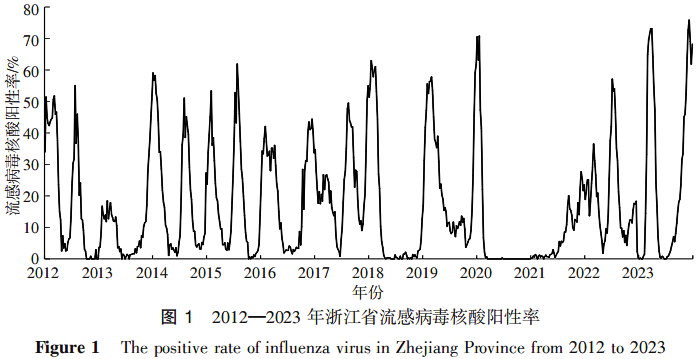
2.1 2012—2023 年浙江省流感流行情况 2012—2023 年浙江省流感整体呈冬春季与夏季双峰流行,夏季峰低于冬春季峰,部分年份夏季峰未出现。2012—2013 年流行季至 2022—2023 年流行季平均流感病毒核酸阳性率分别为 8.40%、25.13%、16.34%、19.29%、27.23%、21.84%、25.64%、19.18%、0.45%、18.15% 和 25.89%。流行株包括 A(H3N2)型、A(H1N1)型和 B 型(以 Victoria 系和 Yamagata 系为主),三者混合交替流行;冬春季流行峰主要由 A(H1N1)型和 B 型引起,夏季流行峰主要由 A(H3N2)型引起。见图 1。
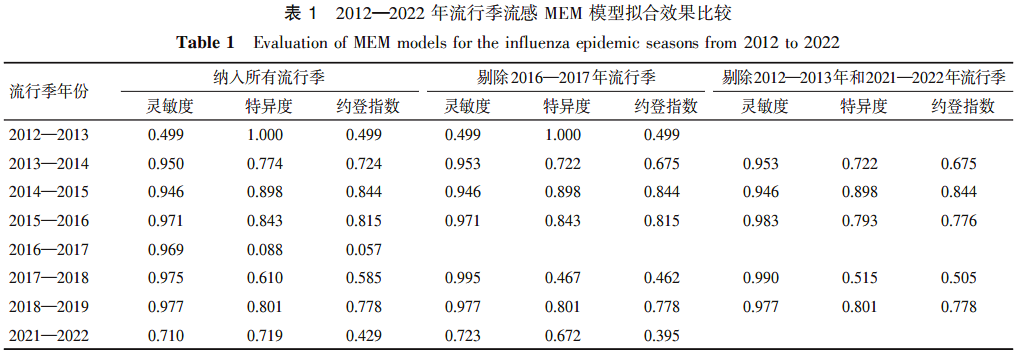
2.2 拟合最优 MEM 模型 各流行季 MEM 模型评价结果显示,2016—2017 年流行季模型的特异度相对较低;将该流行季数据剔除后拟合 MEM 模型,发现 2012—2013 年流行季和 2021—2022 年流行季模型的灵敏度和约登指数与其他流行季的差距较大;剔除 2012—2013 年和 2021—2022 年流行季数据后再拟合 MEM 模型,各流行季模型均表现良好。见表 1。灵敏度、特异度和约登指数综合表现最优时对应的 δ 为 1.5。最终纳入 2013—2014 年、2014—2015 年、2015—2016 年、2017—2018 年和 2018—2019 年 5 个流行季的监测数据,δ 设为 1.5,建立的 MEM 模型为最优模型,其灵敏度为 0.971, 特异度为 0.745,约登指数为 0.716。
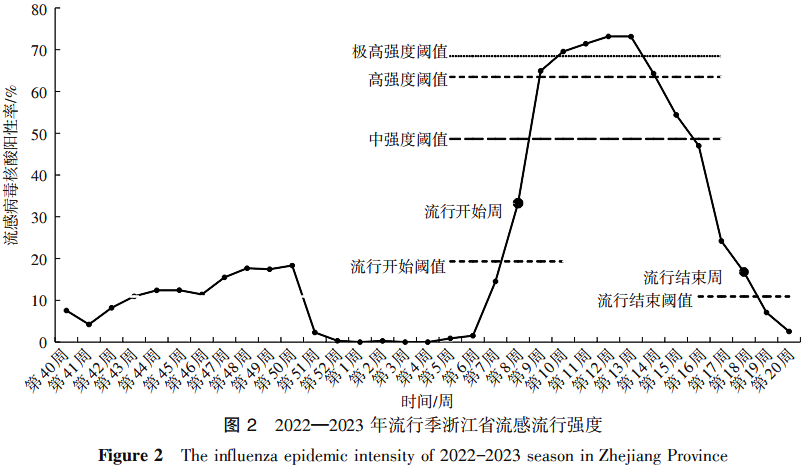
2.3 2022—2023 年流行季浙江省流感流行强度评估 应用最优 MEM 模型,计算得浙江省流感流行开始阈值和结束阈值分别为 19.32% 和 10.92%,中、高和极高强度阈值分别为 48.65%、63.49% 和 68.47%。实际监测的流感病毒核酸阳性率<19.32%(流行前期)或<10.92%(流行后期)为非流行期;19.32%~<48.65% 为低流行强度;48.65%~<63.49% 为中流行强度;63.49%~<68.47% 为高流行强度;≥68.47% 为极高流行强度。由此评估 2022—2023 年流感流行情况:2022 年第 40 周至 2023 年第 7 周的流感病毒核酸阳性率<19.32%,为流行前期,2023 年第 8 周进入低流行强度,第 9 周快速升至高流行强度,第 10—13 周进入极高流行强度,第 14 周回落至高流行强度,第 15 周短暂处于中流行强度,第 16—18 周回落至低流行强度,第 19 周进入流感流行后期。见图 2。
3 讨论
浙江省目前已建成较为成熟的流感监测网络,为实现流感强度分级评估提供了丰富的数据。本研究利用浙江省 2012—2022 年流感监测数据建立 MEM 模型,计算流感流行开始/结束阈值和流行强度分级阈值,对 2022—2023 年全省流感强度进行分级评估。MEM 方法适用于每年单个流行高峰的传染病[5],浙江省流感虽然在部分年份出现了夏季流行小高峰,但仍以冬春季流行高峰为主,且冬春季峰高于夏季峰。流感夏季高峰处于暑假期间,暴发疫情风险低,而冬春季气温低、空间密闭、人群密集,流感防控压力大于夏季,因此出于防控实践考虑,本研究选择流感冬春季流行数据建立 MEM 模型。
本研究建立的流感 MEM 模型灵敏度为 0.971,特异度为 0.745,约登指数为 0.716,与江苏省研究结果(0.946 5、0.863 2、0.809 7)[12]相比,灵敏度较高,特异度和约登指数较低;与北京市研究结果(0.60、0.94、0.54)[13]相比,灵敏度和约登指数较高,特异度较低。灵敏度高,提示该流行阈值准确识别流感进入流行期的能力较强,即更容易识别流感流行;特异度低可导致不能准确识别非流行期,特异度太高又会造成流感流行预警不及时[14-15]。对于流感监测预警而言,能够及时、准确识别流感流行更为重要,因此模型的预测灵敏度要高[14]。
浙江省流感流行开始阈值和结束阈值分别为 19.32% 和 10.92%,与江苏省研究结果(17.27% 和 11.27%)[12]类似;中、高和极高强度阈值分别为 48.65%、63.49% 和 68.47%,高于江苏省研究结果(29.86%、42.31% 和 46.71%)[12]。但与南方其他地区和北方地区相比,流行阈值和强度分级阈值相差较大[11,16-17],提示使用 MEM 对流感流行强度进行分级评估时需考虑地区差异。本研究利用获得的强度分级阈值,评估浙江省 2022—2023 年流行季流感流行强度及不同流行强度的持续时间,结果显示,2022—2023 年流行季流感流行强度变化迅速且剧烈,第 8 周进入低流行强度,第 9 周快速进入高流行强度,第 10—13 周处于极高流行强度且持续时间较长。
建立 MEM 模型获得的流行阈值和强度分级阈值不仅能判断浙江省 2022—2023 年流感流行开始时间,提早部署防控措施,而且利用强度分级阈值评估流感流行季不同时期的流行强度及持续时间,对采取的防控级别、范围和时间具有指导意义。但本研究也存在一定局限性:根据交叉验证结果删除了部分监测数据以提高模型的拟合度,但对最优 MEM 模型的选择也造成了一定影响。
参考文献

